وبلاگ سوالات ریاضی . لگاریتم . توان . سوالات تیمز . ضرب و ..

روی ادامه مطالب کلیک کنید

اموزش رادیکال(3)

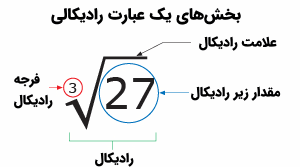
به یاد داشته باشید که می‌توانیم هر عدد را به صورت مربع یا مکعب یا به هر توانی رسانده و سپس از عدد حاصل، جذر، کعب یا رادیکال برحسب فرجه همان توان بگیریم و به عدد اولیه برسیم. این کار را در مثال‌های قبلی دیدیم، در ادامه متن، به مواردی اشاره خواهیم کرد که برای مشخص کردن رادیکال اعداد از عکس عمل توان رساندن استفاده کردیم.

همانطور که می‌دانید، 16 یک عدد مربع است زیرا می‌توان آن را برمبنای توان ۲ نمایش داد.

16=4به توان 2

پس ریشه دوم عدد ۱۶ برابر است با ۴.

√16=4

ولی متاسفانه همیشه نمی‌توان رادیکال را به صورت ساده و برحسب توان، محاسبه کرد. برای مثال مقدار ۳ را در نظر بگیرید. در بین اعداد صحیح، عددی وجود ندارد که آن را به توان ۲ رسانده و به مقدار ۳ برسیم.

3=a2

متاسفانه a

یک عدد صحیح یا حتی گویا نخواهد بود و باید آن را در بین اعداد حقیقی جستجو کرد. اگر با استفاده از ماشین حساب ریشه دوم عدد ۳ را محاسبه کنید به مقدار زیر خواهید رسید.

√3≅1.732050808

عدد حاصل یک عدد گنگ بوده و در نتیجه نمی‌توان مقدار دقیق آن را مشخص کرد. بنابراین در اغلب موارد آن را بوسیله عمل گرد کردن، به نزدیک‌ترین عدد گویا گرد کرده و برای محاسبات به کار می‌گیریم.

از آنجایی که در اغلب موارد با رادیکال با فرجه ۲ یا ریشه دوم اعداد مواجه می‌شویم، بخش بعدی را به نحوه محاسبه این گونه رادیکال‌ها یعنی ریشه دوم اعداد یا عبارت‌های جبری اختصاص می‌دهیم. ولی در قسمت‌های بعدی، نگاهی به رادیکال با فرجه‌های بزرگتر از ۲ نیز خواهیم داشت. یکی از کاربردهای مهم ریشه دوم یا رادیکال با فرجه ۲، در قضیه فیثاغورس (فیثاغورث) نهفته است.

قضیه فیثاغورس: در یک مثلث قائم‌الزاویه، مربع وتر، برابر است با مجموع مربعات دو ضلع دیگر. بنابراین اگر طول ضلع وتر را با c و طول اضلاع دیگر را با a و b‌ نشان دهیم، طبق این قضیه، رابطه زیر برقرار است.

c2=a2+b2

به این ترتیب می‌توانیم طول ضلع وتر را با محاسبه ریشه دوم مجموع مربعات دو ضلع دیگر از این مثلث بدست آوریم.

c=√a2+b2