وبلاگ سوالات ریاضی . لگاریتم . توان . سوالات تیمز . ضرب و ..

ادامه مطالب کلیک کنید

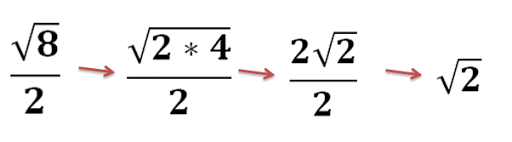
ساده کردن عبارت‌های رادیکال یا جذر

برای ساده سازی عبارتی که حاوی ریشه مربع یا جذر است، باید جملات داخل رادیکال را به صورت «مربع کامل» درآوریم. سپس این بخش را از داخل رادیکال خارج کرده و با گرفتن ریشه دوم از آن، در خارج از رادیکال نمایش دهیم.

به عنوان مثال، مشخص است که عدد 4 همان مربع عدد 2 است، بنابراین ریشه دوم 4 برابر است با ۲، زیرا عدد ۴ از ضرب دو عامل یکسان یا برابر (که در اینجا عدد ۲ است) ساخته شده.

√4=√22=√2×2=2

همانطور که در رابطه بالا مشاهده شد، ابتدا ۴ را به صورت یک مربع کامل (22

) نوشتیم، سپس پایه را از داخل رادیکال خارج کردیم زیرا توان با فرجه رادیکال یکسان است. بنابراین عبارت زیر رادیکال (بدون در نظر گرفتن توان آن) از داخل آن خارج خواهد شد.  همین عمل را برای عدد ۴۹ نیز تکرار می‌کنیم.

√49=√72=√7×7=7

باز هم می‌بینید، چون ۴۹ را می‌توان به صورت 72

نوشت، توان را با فرجه رادیکال ساده کرده و  عدد ۷ را از داخل رادیکال خارج کرده‌ایم. به عنوان یک مورد دیگر به ۲۲۵ اشاره می‌کنیم. می‌دانیم که مربع ۱۵ برابر است با ۲۵۵. بنابراین، ریشه دوم ۲۵۵ همان مقدار ۱۵ خواهد بود. این کار را بوسیله مربع کردن عبارت زیر رادیکال به شکل زیر انجام می‌دهیم، سپس با حذف فرجه با توان، مقدار زیر رادیکال را بیرون می‌آوریم.

√255=√152=√15×15=15

نکته: توجه داشته باشید که مقدار یا نتیجه محاسبه رادیکال، همیشه مقداری مثبت یا نامنفی است. ولی اگر از اعداد منفی چشم پوشی نکرده باشیم، می‌توانیم آن‌ها را در محاسبه مربع نیز به کار ببریم. به رابطه‌های زیر دقت کنید. مشخص است که برای مثال مربع ۲- نبر برابر با ۴ است. ولی هرگز ریشه دوم یا رادیکال ۴ را برابر ۲- قرار نمی‌دهیم. زیرا همیشه مقدار رادیکال با فرجه زوج، مثبت است.

√(−2)2=√−2×(−2)=2

√(−7)2=√−7×(−7)=7

√–152=√−15×(−15)=15

تأکید می‌کنیم که ارزیابی یک عبارت برای یافتن مقدار و حل یک معادله به منظور پیدا کردن ریشه‌های آن، دو چیز کاملاً متفاوت هستند. در حالت اول، درست به مانند عملیات قسمت قبل عمل می‌کنیم و برای مثال هرگز ریشه دوم مقدار ۴ را با علامت منفی نشان نمی‌دهیم. ولی اگر برای حل معادله x2=4

اقدام کنیم، ریشه‌ها را به  ترتیب برابر با ۲ و ۲- در نظر می‌گیریم. زیرا می‌دانیم، مربع ۲ یا ۲- برابر با ۴ هستند. به این ترتیب به دنبال همه مقادیری هستیم که در معادله صدق می‌کنند. پس برای این معادله دو ریشه حقیقی پیدا می‌کنیم که تساوی برایشان برقرار می‌شود.

همین موضوع نشان می‌دهد که محاسبه با حل معادله درجه ۲ ممکن است تفاوت‌های زیادی داشته باشند. رابطه‌های زیر را در این حالت در نظر بگیرید.

(−2)2=4,22=4

(−3)2=9,32=9

(−5)2=25,52=25

(−7)2=49,72=49

همانطور که در مثال مربوط به ریشه دوم عدد ۳ اشاره کردیم، اغلب اوقات بدست آوردن نتیجه یک رادیکال به کمک تبدیل به مربع کامل امکان‌پذیر نیست، اما ممکن است یک مربع در میان عوامل آن وجود داشته باشد. برای ساده سازی این نوع رادیکال‌ها، ما باید استدلال را به کمک فاکتور گیری صورت دهیم. یعنی هر آنچه درون رادیکال است را با توجه به عواملی که به صورت مربع هستند، فاکتور گیری کرده، سپس به ساده‌سازی رادیکال دست بزنیم.

هنگام انجام این کار، استفاده از این واقعیت مهم است که می‌توانیم ضرب رادیکال‌ها را به صورت رادیکال ضرب جملات داخل رادیکال بنویسیم. این موضوع درست مشابه توان رسانی و روش‌هایی ساده کردن جملات توان‌دار است. به قواعد زیر توجه کنید.

قاعده ضرب جملات توان‌دار و توان‌دار کردن ضرب آن‌ها

(ab)n=an×bn

به این ترتیب براساس رابطه بالا، برای رادیکال نیز رابطه زیر برقرار است.

قاعده تبدیل ضرب رادیکال به رادیکال ضرب و برعکس

n√ab=n√an√b

در ادامه برای نشان دادن کاربرد این قاعده، مثال‌هایی ذکر خواهیم کرد که به درک عملیات مربوط به ساده‌سازی رادیکال‌ها کمک خواهند کرد.

مثال‌های مربوط به ساده‌سازی رادیکال

در مثال‌های پیش رو به وضعیتی خواهیم پرداخت که از قواعد ساده سازی گفته شده در قسمت قبل، برای محاسبه رادیکال استفاده خواهیم کرد.

مثال ۱: مقدار √144

را محاسبه کنید.

برای بدست آوردن رادیکال بالا، از دو شیوه کمک می‌گیریم. ابتدا ۱۴۴ را به صورت حاصل‌ضرب دو عبارت مربع می‌نویسیم. مشخص است که رابطه زیر بین ۱۴۴ با ۹ و ۱۶ برقرار است.

144=9×16

می‌دانیم که ۹ و ۱۶ هر دو مربع کامل هستند.  پس عبارت زیر رادیکال را به به صورت حاصل‌ضرب این دو مقدار یعنی مربع کامل می‌نویسیم.

√144=√9×16=√9×√16=3×4=12

می‌توان مشاهده کرد که از تبدیل رادیکال ضرب به ضرب رادیکال بهره برده‌ایم.

راه حل دوم آن است که به طور مستقیم، ۱۴۴ را به صورت مربع کامل بنویسیم. همانطور که می‌دانید مربع ۱۲ برابر است با ۱۴۴، پس در این حالت ۱۲ ریشه دوم ۱۴۴ خواهد بود.

√144=√122=12

مثال ۲: عبارت √24×√6

را ساده کنید.

این‌بار هم از قاعده تبدیل ضرب رادیکال‌ها به رادیکال ضرب استفاده می‌کنیم و نتیجه را بدست می‌آوریم.

√24×√6=√24×6=√144=12

واضح است که برای بدست آوردن تساوی آخر، به مثال ۱ توجه داشته‌ایم.

مثال ۳: مقدار √75

را به ساده‌ترین حالت مشخص کنید.

این بار عدد ۷۵ را به صورت تجزیه به عوامل اول در می‌آوریم. به این ترتیب رابطه یا تساوی زیر حاصل می‌شود.

75=3×5×5

منظور از تجزیه به عوامل اول، نوشتن یک عدد، برحسب ضرب اعدادی است که همگی عدد اول باشند.

بنابراین برای محاسبه √75

از این تجزیه کمک می‌گیریم.

√75=√3×5×5=√3×52

از آنجایی که عبارت 52

یک عبارت یا جمله مربع کامل است، پایه آن از داخل رادیکال خارج می‌شود و خواهیم داشت:

√75=√3×5

البته در اغلب موارد دوست داریم که عدد را بر رادیکال مقدم بداریم به همین دلیل ۵ را به صورت ضریب در ابتدای عبارت نوشته و رادیکال را به عنوان عبارت دوم در ضرب به کار می‌بریم تا به اشتباه رابطه بالا را به صورت √35

به کار نبریم.

√75=5√3

نتیجه سمت راست تساوی بالا را به صورت «پنج رادیکال ۳» می‌خوانیم.

نکته: هنگام نوشتن یک عبارت حاوی رادیکال، فرم مناسب آن است که رادیکال را در انتهای عبارت قرار دهید. ولی باید توجه داشته باشید که عدد قبل از رادیکال را با فرجه رادیکال اشتباه نگیرید. بنابراین همیشه مراقب باشید که فرجه را درست بالای علامت رادیکال قرار دهید تا دچار اشتباه نشوید.

هنگام ساده سازی لازم نیست که عبارت زیر رادیکال را تا انتهای اعداد اول فاکتور بگیرید. به محض اینکه می‌بینید یک عامل یا مضربی به شکل مربع کامل دارید و آنچه باقی می‌ماند، قابلیت تبدیل به مربع کامل را ندارد، دست نگه داشته و نتیجه را به صورت حاصل ضرب نمایش می‌دهیم.

مثال ۴: √72

را به ساده‌ترین حالت بنویسید.

ابتدا سعی می‌کنیم بخش مربع کامل را از ۷۲ استخراج کنیم.

√72=√2×36=√2×62=6√2

همانطور که مشخص است از مربع کامل یعنی عدد ۳۶ در تجزیه ۷۲ کمک گرفته و نتیجه را به صورت ضرب عدد در رادیکال نمایش دادیم.

نکته: توجه دارید که ۲ مربع کامل نیست و از رادیکال خارج نمی‌شود.

مثال ۵: مقدار √4500

را مشخص کنید.

ابتدا با فاکتورگیری آغاز می‌کنیم. از آنجایی که در عدد ۴۵۰۰، به تعداد ۴۵ دسته ۱۰۰ تایی وجود دارد (۱۰۰ نیز مربع کامل است) عبارت را به صورت زیر تجزیه می‌کنیم.

4500=45×100

از نتیجه حاصل برای محاسبه رادیکال استفاده خواهیم کرد. در گام دوم سعی می‌کنیم که ۴۵ را به صورت حاصل‌ضرب عبارت‌های مربع کامل بنویسیم. پس می‌توان نوشت:

45=5×9

پس در حالت کلی از رابطه زیر استفاده خواهیم کرد.

√4500=√45×100=√45×√100=√5×9×10=√5×32×10=3×10×√5=30√5

می‌دانید که منظور از 30√5

همان حاصل‌ضرب ۳۰ در رادیکال ۵ است ولی نمایش آن را بدون علامت ضرب انجام می‌دهیم.

در بخش بعدی به بررسی جملات و عبارت‌های جبری و ریشه دوم آن‌ها خواهیم پرداخت. مشخص است زمانی که از عبارت‌های جبری صحبت می‌کنیم، پای متغیرها نیز در میان خواهد بود. از آنجایی که متغیرها نیز نماینده اعداد هستند، ریشه‌گیری یا محاسبه جذر عبارت های جبری به مانند اعداد خواهد بود. ولی برای تاکید و همچنین استفاده از بعضی اتحادها، جذر گیری یا ساده‌کردن این گونه عبارت‌ها را بازگو خواهیم کرد.