وبلاگ سوالات ریاضی . لگاریتم . توان . سوالات تیمز . ضرب و ..

در بخش قبل دیدید که برای ضرب دو عبارت که به صورت جمع رادیکال‌ها نوشته شده، باید از خاصیت پخشی ضرب نسبت به جمع استفاده کنید. ولی در بسیاری از موارد به کمک اتحادها، بخصوص اتحاد مزدوج، این ضرب‌ها به سادگی قابل حل هستند.

البته برای آنکه ابتدا بدانیم چگونه این ضرب‌ها باید صورت گیرند، همان خاصیت پخشی را به کار برده ولی ضرب‌ها را به صورت ستونی یا عمودی انجام می‌دهیم. این عمل ضرب را هنگامی که اعداد دو رقمی را ضرب می‌کنیم هم به کار برده‌ایم. در ادامه این نوع ضرب را به کمک مثال‌هایی، معرفی می‌کنیم.

مثال ۲۲: حاصل ضرب √3+√5

را در √3–√6

مشخص کنید.

قاعده ضرب عمودی را برای تک تک جمله‌ها به کار خواهیم برد. به تصویر زیر دقت کنید.

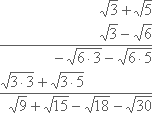
همانطور که می‌بینید، قسمت اول ضرب در بخش اول دیده می شود و بخش دوم (سطر دوم) از ستون دوم آغاز شده. همین عملیات را به صورت پخشی و سطری نیز می‌توان اجرا کرد.

(√3+√5)(√3–√6)=√9+√15–√18–√30=3+√15–√9×2–√30

پس از ساده‌سازی و جمع جبری جملات مشابه به رابطه زیر خواهیم رسید.

3+√15–3√2–√30

مثال ۲۳: ضرب زیر را انجام دهید.

(√3+√5)(√3–√5)

می‌بینید که پرانتز اول بسیار به پرانتز دوم شبیه است. در حقیقت تنها تفاوت در علامت جمع و تفریق دو پرانتز نهفته است. در این حالت عبارت اول و دوم را «مزدوج» (Conjugate) یکدیگر می‌نامند. در اینجا عمل ضرب را به مانند قبل انجام می‌دهیم ولی در ادامه مفهوم ضرب عامل‌های مزدوج را به کمک اتحادها اجرا خواهیم کرد.

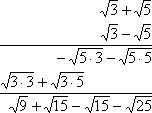
در ضرب بالا که به صورت ستونی نوشته شده، مشخص است که عبارت‌ها، یکی یکی در هم ضرب و سپس با هم جمع شده‌اند. پس از جمع جبری به رابطه زیر خواهیم رسید.

(√3+√5)(√3–√5)=√9+√15–√15–√25=√9–√25=3−5=−2

نکته: هر دو عبارت اولیه، یک عدد غیرگویا (عدد موهومی) را نشان می‌دهند در حالیکه حاصل‌ضرب آن‌ها یک عدد گویا (۲-) شد. این امر نشان می‌دهد که از ضرب دو عدد موهومی می‌توان یک عدد گویا ساخت ولی به یاد داشته باشید که از ضرب دو عدد گویا، یک عدد موهومی یا گنگ حاصل نمی‌شود.

بر روی ادامه مطالب کلیک کنید