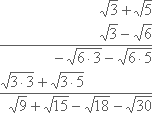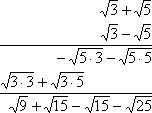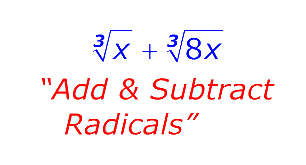وبلاگ سوالات ریاضی . لگاریتم . توان . سوالات تیمز . ضرب و ..

در بخش قبل دیدید که برای ضرب دو عبارت که به صورت جمع رادیکال‌ها نوشته شده، باید از خاصیت پخشی ضرب نسبت به جمع استفاده کنید. ولی در بسیاری از موارد به کمک اتحادها، بخصوص اتحاد مزدوج، این ضرب‌ها به سادگی قابل حل هستند.

البته برای آنکه ابتدا بدانیم چگونه این ضرب‌ها باید صورت گیرند، همان خاصیت پخشی را به کار برده ولی ضرب‌ها را به صورت ستونی یا عمودی انجام می‌دهیم. این عمل ضرب را هنگامی که اعداد دو رقمی را ضرب می‌کنیم هم به کار برده‌ایم. در ادامه این نوع ضرب را به کمک مثال‌هایی، معرفی می‌کنیم.

مثال ۲۲: حاصل ضرب √3+√5

را در √3–√6

مشخص کنید.

قاعده ضرب عمودی را برای تک تک جمله‌ها به کار خواهیم برد. به تصویر زیر دقت کنید.

همانطور که می‌بینید، قسمت اول ضرب در بخش اول دیده می شود و بخش دوم (سطر دوم) از ستون دوم آغاز شده. همین عملیات را به صورت پخشی و سطری نیز می‌توان اجرا کرد.

(√3+√5)(√3–√6)=√9+√15–√18–√30=3+√15–√9×2–√30

پس از ساده‌سازی و جمع جبری جملات مشابه به رابطه زیر خواهیم رسید.

3+√15–3√2–√30

مثال ۲۳: ضرب زیر را انجام دهید.

(√3+√5)(√3–√5)

می‌بینید که پرانتز اول بسیار به پرانتز دوم شبیه است. در حقیقت تنها تفاوت در علامت جمع و تفریق دو پرانتز نهفته است. در این حالت عبارت اول و دوم را «مزدوج» (Conjugate) یکدیگر می‌نامند. در اینجا عمل ضرب را به مانند قبل انجام می‌دهیم ولی در ادامه مفهوم ضرب عامل‌های مزدوج را به کمک اتحادها اجرا خواهیم کرد.

در ضرب بالا که به صورت ستونی نوشته شده، مشخص است که عبارت‌ها، یکی یکی در هم ضرب و سپس با هم جمع شده‌اند. پس از جمع جبری به رابطه زیر خواهیم رسید.

(√3+√5)(√3–√5)=√9+√15–√15–√25=√9–√25=3−5=−2

نکته: هر دو عبارت اولیه، یک عدد غیرگویا (عدد موهومی) را نشان می‌دهند در حالیکه حاصل‌ضرب آن‌ها یک عدد گویا (۲-) شد. این امر نشان می‌دهد که از ضرب دو عدد موهومی می‌توان یک عدد گویا ساخت ولی به یاد داشته باشید که از ضرب دو عدد گویا، یک عدد موهومی یا گنگ حاصل نمی‌شود.

درست مانند اعداد گویا، ریشه‌ها یا اعداد رادیکالی را می‌توان با هم جمع یا تفریق کرد. البته ممکن است عمل ساده‌سازی نتیجه جمع یا تفریق قابل اجرا نباشد. از طرفی به این موضوع نیز توجه داشته باشید که رادیکال‌ها برای جمع یا تفریق باید دارای فرجه یکسانی بوده و در عین حال، مقدار زیر رادیکال نیز برایشان برابر باشد.

به این ترتیب باید جملات مشخص برای جمع و تفریق رادیکالی، مشابه باشند. پس بهتر است تعریفی از اعداد یا عبارت‌های رادیکالی مشابه ارائه دهیم. زیرا دو عدد رادیکالی را زمانی می‌توان با یکدیگر جمع جبری کنیم که مشابه باشند.

رادیکال های مشابه: اعداد رادیکال‌دار، زمانی مشابه هستند که فرجه و مقدار زیر رادیکال در آن‌ها برابر بوده و تنها می‌تواند ضریب رادیکال‌ها با یکدیگر تفاوت داشته باشند. در جمع و تفریق اعداد رادیکالی این موضوع اهمیت پیدا می‌کند زیرا فقط رادیکال های مشابه را می‌توان از هم تفریق یا با هم جمع کرد.

برای مثال 5√3

و 4√3

مشابه هستند، زیرا فرجه هر دو رادیکال ۲ بوده و از طرفی مقدار زیر رادیکال در هر دو عدد برابر با ۳ است. اعداد ۴ و ۵و نیز ضریب‌های رادیکال‌ها هستند. بنابراین اگر قرار باشد آن‌ها را با یکدیگر جمع یا تفریق کنیم، رابطه‌ها را به صورت زیر خواهیم نوشت.

4√3+5√3=9√3

همچنین برای تفریق نیز به صورت زیر عمل خواهیم کرد.

4√3–5√3=−1√3

بنابراین قاعده کلی برای جمع یا تفریق دو عدد رادیکال (ریشه دوم) با ضرایب مختلف را به صورت زیر خواهیم داشت:

a√x±b√x=(a±b)√x

همچنین یکسان بودن فرجه‌ها را هم باید در نظر گرفت. برای مثال اگر ریشه n

ام عدد x

مطرح باشد، رابطه بالا به صورت کلی به شکل زیر خواهد بود.

an√x±bn√x=(a±b)n√x

نکته: اگر در عبارت اول، فرجه n

و در عبارت دوم، فرجه m بوده که n≠m، آنگاه امکان جمع‌کردن این جمله وجود نخواهد داشت. همچنین اگر در عبارت اول x و در عبارت دوم y‌ مقدار زیر رادیکال باشند، بطوری که x≠y

آنگاه امکان جمع جبری جملات وجود ندارد.

در ادامه به ذکر مثال‌هایی در این زمینه می‌پردازیم تا مسئله جمع و تفریق رادیکال برایتان روشن‌تر شود.

مثال ۱۳: عبارت زیر را ساده کنید.

2√3+3√3

از آنجایی که هر دو عبارت در جمع، رادیکال با فرجه ۲ هستند و مقدار زیر رادیکال نیز یکسان است، امکان محاسبه جمع جبری وجود دارد. در این حالت به صورت زیر عمل می‌کنیم.

2√3+3√3=(2+3)√3=5√3

مثال ۱۴: نتیجه جمع رادیکال ۹ و رادیکال ۲۵ چیست؟

در حقیقت مسئله را به بیان ریاضی به شکل زیر مشخص می‌کنیم.

√9+√25=3+5=8

نکته: توجه داشته باشید که در رابطه بالا، ابتدا رادیکال‌ها ساده شده، سپس با یکدیگر جمع شده‌اند. واضح است که رابطه زیر را برای جمع کردن رادیکال‌ها نباید به کار بست.

√x+√y≠√x+y

مثلا طبق مثال ۱۴، داریم:

√9+√25=3+5=8≠√9+25=√34≅5.83

ولی به این موضوع نیز توجه داشته باشید که ممکن است با ساده کردن رادیکال‌هایی مانند √x

یا √y

، به عبارت‌هایی برسیم که در زیر رادیکال، مقدارهای زیر رادیکال برابر شده و با توجه به یکسان بودن فرجه‌ها، جمع یا تفریق میسر شود. مثال‌های قبلی به این موضوع پرداخته بودند. در ادامه به مثال‌های دیگری اشاره می‌کنیم که در آن‌ها، یا جملات مشابه وجود دارند یا به کمک تغییراتی می‌توان به جملات مشابه برای محاسبه رادیکال، رسید.

مثال ۱۵: نتیجه جمع زیر را بدست آورید.

3√4+2√4

از آنجایی که عبارت‌های زیر رادیکال برابر بوده و هر دو برحسب ریشه دوم هستند، امکان جمع کردن وجود دارد. پس نتیجه را به صورت زیر محاسبه می‌کنیم.

3√4+2√4=(3+2)√4=5×2=10

مثال ۱۶: نتیجه جمع برای عبارت زیر چیست؟

3√3+2√5+√3

همانطور که می‌بینید فقط دو جمله اول و سوم در این مثال مشابه هستند و به این ترتیب 3√3

و √3 قابل جمع بوده و عبارت 2√5

نمی‌تواند با آن‌ها جمع شود.

3√3+2√5+√3=3√3+√3+2√5=(3+1)√3+2√5=4√3+2√5

واضح است که ضریب در عبارت سمت چپ، یعنی √3

برابر با ۱ است. به همین دلیل در ادامه محاسبات، داخل پرانتز، ۱ را با ۳ جمع کرده‌ایم. در مثال بعدی می‌خواهیم به موارد بیشتری از نحوه جمع یا تفریق جملات رادیکالی بپردازیم.

مثال ۱۷: عبارت زیر را ساده کنید.

√18−2√27+3√3−6√8

برای آنکه به ساده‌ترین حالت نمایش این جمع و تفریق برسیم، مراحل زیر را طی خواهیم کرد.

√18−2√27+3√3−6√8=√2×32–2√33+3√3–6√23

به این ترتیب با ساده کردن رادیکال‌ها به رابطه زیر خواهیم رسید.

√2×32–2√33+3√3–6√23=3√2–2×3√3+3√3–6×2√2

که پس از ساده‌سازی و جمع جبری رادیکال‌ها مقدار نهایی بدست می‌آید.

3√2–2 ×3√3+3√3–6×2√2=3√2–12√2–6√3+3√3=−9√2–3√3

همانطور که در این مثال مشاهد کردید، در ابتدا به نظر می‌رسید با نابرابری مقادیر زیر رادیکال، امکان جمع یا تفریق وجود ندارد. ولی پس از آنکه عبارت‌های رادیکالی را ساده کردیم، به جملات مشابه رادیکالی رسیدیم و توانستیم محاسبات مربوط به جمع و تفریق را برای این جمله‌ها اجرا کنیم.

مثال ۱۸: نتیجه ساده‌سازی رابطه 2√3+3√5

چه خواهد شد؟

از آنجایی که هر دو رادیکال فرجه یکسانی دارند، امکان ساده‌سازی و جمع کردن آن‌ها محتمل است. ولی از طرفی، مقادیر زیر رادیکال‌ها یکسان نیستند و امکان ساده‌سازی نیز وجود ندارد. بنابراین عبارت گفته شده به ساده‌ترین شکل نوشته شده و نمی‌توان در آن تغییری بوجود آورد.

مثال ۱۹: حاصل ضرب √2

در (3+√3)

را بدست آورید.

از خاصیت پخشی ضرب نسبت به جمع استفاده کرده و رابطه ضرب را ساده می‌کنیم.

√2(3+√3)=√2(3)+√2(√3)=3√2+√2×3=3√2+√6

همانطور که مشخص است، نتیجه از این ساده‌تر نخواهد شد.

مثال ۲۰: حاصل ضرب √3(2√3+√5)

چیست؟

√3(2√3+√5)=√3(2√3)+√3(√5)=2×√3×3+√3×5=2×3+√15=6+√15

مثال ۲۱: مقدار حاصل ضرب زیر را بدست آورید.

(1+√2)(3–√2)

در این مثال به کمک ضرب جمله به جمله، محاسبات را برای مقادیر رادیکالی اجرا می‌کنیم و هر بار بخشی از عبارت اول را به صورت پخشی، در عبارت دوم ضرب خواهیم کرد.

(1+√2)(3–√2)=(1)×(3–√2)+√2(3–√2)=3−√2+3×√2–(√2×√2)=3–√2+3√2–2=3+2√2−2=1+2√2