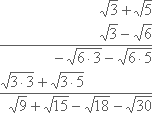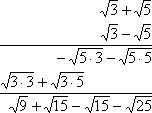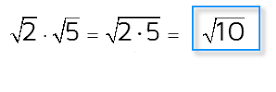هنگام ساده سازی عبارتهای زیر رادیکال، شما همیشه فقط اعداد درون رادیکال را نخواهید داشت. ممکن است یک عبارت رادیکالی با متغیرها نیز همراه باشد. متغیرهای موجود در محاسبه یک رادیکال به همان روش اعداد صورت خواهد گرفت و مبنا، ایجاد جملاتی به صورت مربع کامل یا فاکتورگیری است. برای توضیح مراحل کار به ذکر مثالهایی در این زمینه خواهیم پرداخت.
مثال ۶: عبارت √16x4
را ساده کنید.
از قبل میدانیم که 16 یک مربع کامل است، بنابراین عدد 4 را از رادیکال خارج میکنیم. با نگاه به بخش متغیر، متوجه میشویم که x نیز به صورت مربع کامل به کار رفته است. بنابراین میتوانیم از متغیر را هم از رادیکال خارج کنیم.
به روند مربوط به این محاسبه که در ادامه دیده میشود، توجه کنید.
√16x2=√42×(x2)2
عبارتهای طرف راست، مربع کامل هستند و پایهها از رادیکال خارج میشوند.
√16x4=4×x2=4x2
همانطور که میبینید، سادهسازی رادیکالهایی که شامل متغیرها هستند دقیقاً به همان روش سادهسازی رادیکالهایی است که فقط شامل اعداد هستند. فاکتور گیری یا تبدیل به مربع کامل، راهکارهایی است که در اینجا نیز به کار میروند.
مثال ۷: عبارت √12a4b7c3
را ساده کنید.
از آنجایی که فرجه رادیکال زوج است (اگر رادیکال بدون فرجه باشد، محاسبه ریشه دوم صورت میگیرد) بنابراین تمامی جملات با توان زوج را میتوان به صورت مربع کامل در آورد و از رادیکال خارج کرد. همچنین برای جمله یا عبارتهایی به شکل توانهای فرد نیز میتوان بخشی را به صورت توان زوج و بخش دیگر را به صورت توان فرد در آورد که حاصل ضرب آنها، همان توان عبارت اصلی را بسازد.
همانطور که مشخص است b و c دارای توانهای فرد هستند ولی میتوانیم آنها را به دو بخش ضربی با توانهای زوج و فرد تفکیک کنیم. محاسبات را در ادامه میبینید.
√12a4b7c3=√3×22×a2×a2×(b3)×(b3)×b×c2×c=√3×(a2)2×(b3)2×b×c2×c
به این ترتیب با خارج کردن عبارتهای مربع کامل، جملات سمت راست ساده شده و به شکل زیر در میآیند.
2×a2×b3×c×√3×b×c=2a2b3c√3bc
باز هم میبینید که با ضربکردن اعداد، اعداد را قبل از عبارت رادیکالی قرار دادهایم تا خواندن جمله، سادهتر شود. به این ترتیب حاصل را به صورت «دو آ دو، بی سه ،سی در رادیکال سه بی سی» میخوانیم.
مثال ۸: عبارت √20r18st21
را ساده کنید.
به وسیله فاکتورگیری و استفاده از تفکیک توانها عبارتهای مربوط به متغیرهای r و s را جدا کرده تا به صورت مربع کامل درآیند. این عملیات در رابطههای زیر اجرا شدهاند.
√20r18st21=√4×5×r18×s×t20×t=2r9t10√5st
نکته: ممکن است اشاره شده باشد که مقدار متغیرهای s , t مثبت هستند. این امر به جهت مثبت بودن مقدار زیر رادیکال مهم است. به یاد دارید که مقادیر زیر رادیکالهای با فرجه زوج، همیشه باید مثبت باشند.
ضرب رادیکال ها
اولین کاری که برای سادهسازی رادیکالها به کار بردید، استفاده از تبدیل رادیکال ضرب به ضرب رادیکالها بود. حال میخواهیم عمل عکس را انجام دهیم و برای سادهسازی ضرب رادیکالها، آنها را به رادیکال ضرب تبدیل کرده و جملهها را ساده کنیم.
ساده سازی رادیکالهای ضرب شده بسیار ساده است، ما از این واقعیت استفاده میکنیم که ضرب دو رادیکال همان رادیکال ضرب است و بالعکس. برای روشن شدن موضوع به ذکر مثالهایی خواهیم پرداخت.
مثال 9: حاصل ضرب √2√8
را انجام دهید.
همانطور که میدانید، این ضرب رادیکالها است و چون فرجه رادیکالها یکسان است میتوانیم ضرب رادیکالها را به صورت رادیکال ضرب عبارتهای زیر رادیکال بنویسیم.
√2√8=√2×8=√16=4
همین عمل را به کمک تجزیه نیز میتوانیم اجرا کنیم. به روابطی که در زیر قابل مشاهده است دقت کنید.
√2×√8=√2×√4×2=√2×2√2=2(√2×√2)=2(√2)2=2×2=4
کاملا مشخص است که ابتدا ۸ را تجزیه کردهایم و به عاملی به صورت مربع درآوردهایم. سپس ضرب دو رادیکال یکسان را ساده کرده و چون هر دو عبارت رادیکالی یکسان هستند، رادیکال را برداشتهایم.
نکته: همانطور که در مثال قبل مشاهده کردید، هنگامی که یک رادیکال به توان ۲ (مثل √22
) برسد، رادیکال از بین میرود. بنابراین میتوان گفت که چه مقدار زیر رادیکال یا کل عبارت (با رادیکال) به توان ۲ برسد، رادیکال از بین خواهد رفت.
مثال ۱۰: عبارت √3√6
با چه مقداری برابر است؟
به منظور محاسبه عبارت گفته شده، ابتدا ضرب رادیکالها را به رادیکال ضرب تبدیل میکنیم.
√3√6=√3×6=√3×(3×2)=√32×2=3√2
مثال ۱۱: عبارت √6√15√10
را ساده کنید.
درست به مانند مراحل قبلی، اعداد را به صورت تجزیه به عوامل اول یا مربع کامل در میآوریم.
6=2×3
15=3×5
10=2×5
بنابراین جذر یا ریشه حاصل ضرب را مینویسیم.
√6√15√10=√6×15×10=√(2×3)×(3×5)×(2×5)=√22×32×52=2×3×5=30
مثال ۱۲: عبارت √4x√5x3
را ساده کنید.
میبینید که در کنار اعداد از متغیرها نیز استفاده شده است. مشخص است که ۴ خود یک مربع کامل است و از درون حاصل ضرب x3
در x
نیز میتوان بخش مربع کامل را استخراج کرد. بنابراین محاسبات را به صورتی که در ادامه میبینید، پی میگیریم.
√4x√5x3=√4x×√5x3=√(4x)×(5x3)=√4×5×x4=2×x2×√5=2x2√5
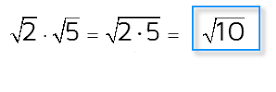
جذر و ریشه اعداد بخصوص در هنگامی که بخواهیم معادله درجه ۲ را حل کنیم، به کار گرفته میشود. در یکی از آموزشهای فرادرس که مختص دبیرستان است، موضوع حل معادله درجه ۲ و به کارگیری جذر معرفی شده است. برای مشاهده این فیلم آموزشی، به لینکی که در ادامه دیده میشود، مراجعه کنید.
 21 اسفند 1401 · ·
21 اسفند 1401 · ·